Solving a Simplified Set of Equations

A linear combination of vector by scalars brings us to our next important topic:
A system of Linear Equations.

In this Linear Algebra lesson we will dive only into a system of two linear equations with two unknowns.

In a broader Linear Algebra class you will find more information about a system of n linear equations, where n can be any number.

Assume that we have two vectors:

• \vec{x}=\begin{bmatrix} -14\\2\end{bmatrix}

• \vec{y}=\begin{bmatrix} 5\\-1\end{bmatrix}

and we would like to represent a new vector:
\begin{bmatrix} -13\\3\end{bmatrix} as a linear combination of \vec{x} and
\vec{y}.

In other words, we are looking for a two scalars, lets call them a and b, that will hold the following equation:

a\begin{bmatrix} -14\\2\end{bmatrix}+b\begin{bmatrix} 5\\-1\end{bmatrix}=\begin{bmatrix} -13\\3\end{bmatrix}

Equation 9

We now know how to multiply a vector by a scalar, so lets do that:

\begin{bmatrix} (-14)a\\2a\end{bmatrix}+\begin{bmatrix} 5b\\(-1)b\end{bmatrix}=\begin{bmatrix} -13\\3\end{bmatrix}

Equation 10

The equation above will give us two separate equations:

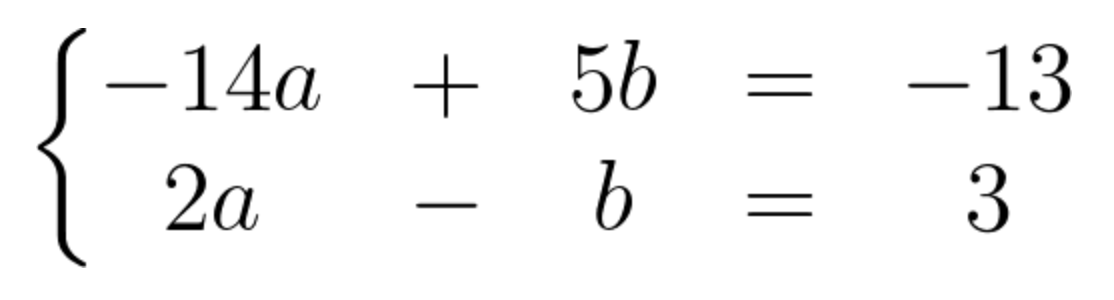
The Above set of equations is referred to in literature as a set of two equations with two unknowns.

This set can be solved using three theoretical methods:

• Graphical method
• Substitution method
• Elimination method

We will go through all methods here.

Graphical solution:

Draw both lines (linear plots) and find the intersection.

The intersection is the solution to (a,b) as it is the only point on both lines. Or, in other words, it is the only point that satisfied both equations.

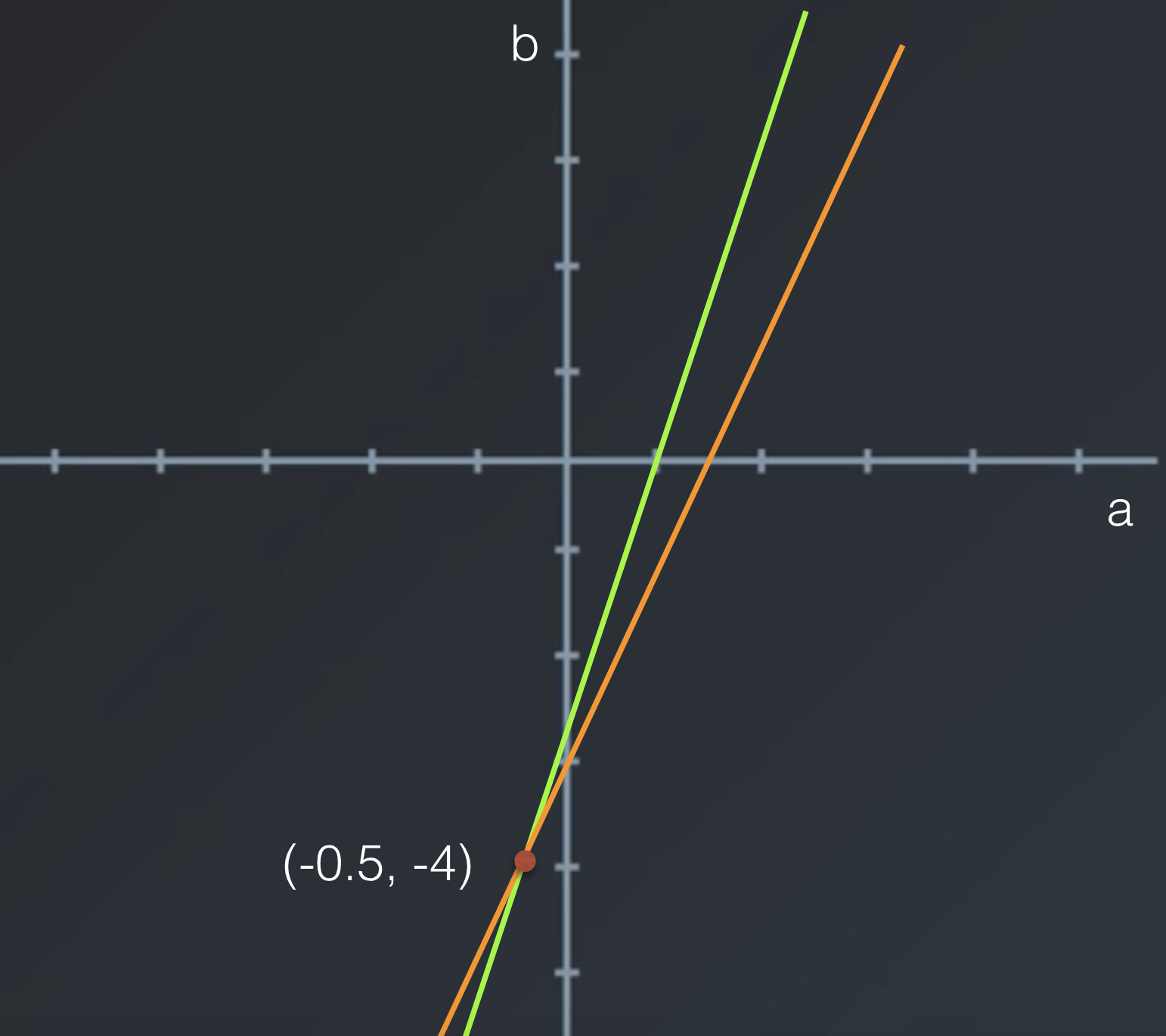
We can clearly see that:

a= -0.5

and

b= -4

Substitution:

Isolate a variable from one of the equations and substitute it in the second.

This method will reduce our system of equations to a single equation with a single unknown.

In our example:

(1) -14a+5b=-13

(2) 2a-b=3

from (1) 2a-b=3\Rightarrow b=2a-3

Substitute b in equation (2)

-14a+5(2a-3)=-13 and solve for a .

Simple algebra will result in a=-0.5

Substitute a in equation (1) or (2) above and you will find that b=-4.

Elimination:

In this method we will eliminate one of the variables, by enforcing the same absolute value to one of the scalars (or coefficients) .

Let's look at the equations again:

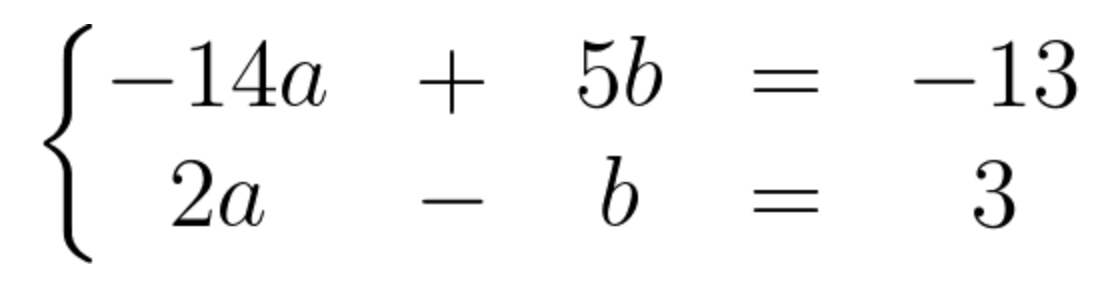
If we multiply equation 2 by 5 we will have the following set of equations:

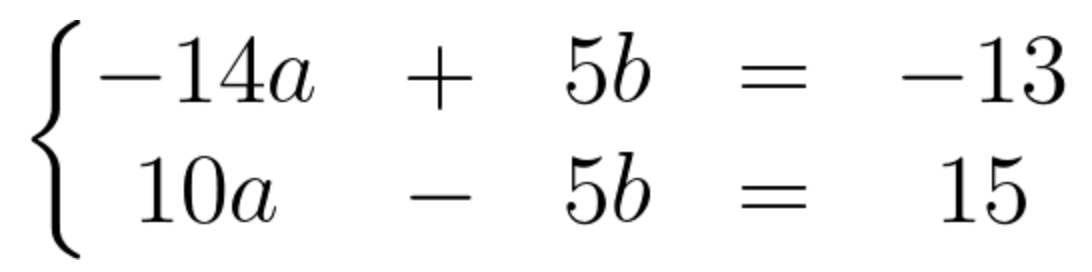
(Notice the the absolute value of the scalar multiplying b, the coefficient of b, is 5 on both equations).

Now let's add them up.

We will have the following single equation with a single unknown:

-4a+0b=2

or:

-4a=2\Rightarrow a=-0.5

Substitute a in any of the equations and you will find that b=-4.

Final answer:

We found scalars a and b that represent vector
\begin{bmatrix} -13\\3\end{bmatrix} as a linear combination of \vec{x} and
\vec{y}.

a\begin{bmatrix} -14\\2\end{bmatrix}+b\begin{bmatrix} 5\\-1\end{bmatrix}=\begin{bmatrix} -13\\3\end{bmatrix}

The single solution is:

a=-0.5 and
b=-4

In this example, one coefficient was positive and the other was negative. Ask yourself, what would you have done if they were both positive, or both negative?

Let's think about another question:

Will a set of two linear equations with two unknowns always have a solution? And if so, will it always be a single solution?

The next set of quizzes will help us answer this question.